Les macros fonctions
Une macro est une fonction dont la forme générale est
fonction nom_fonction(parametres) ;
script tep (pouvant utiliser les parametres)
retourne nom_du_dernier_objet_créé ;
Cette fonction est appelée à partir du script principal à l’aide de la commande :
objet = nom_fonction(parametres) {options} ;
![]() Une fonction peut appeler une autre fonction.
Une fonction peut appeler une autre fonction.
![]() Les fonctions ne peuvent pas créer l’objet var.
Les fonctions ne peuvent pas créer l’objet var.
![]() Au lancement de TracenPoche, celui-ci charge base.txt.
base.txt ne peut contenir des fonctions.
Au lancement de TracenPoche, celui-ci charge base.txt.
base.txt ne peut contenir des fonctions.
D’une manière générale, le permier fichier ouvert à l’aide de TeP ne peut contenir de fonctions pour l’instant.
Syntaxe et appel des fonctions
Exemple 1
fonction mediane(A,B,C) ;
// mediane issue de A dans le triangle ABC ;
I=milieu(B,C) ;
s=segment(A,I) ;
retourne s ;fonction gravite(A,B,C) ;
s = mediane(A,B,C) ;
t = mediane(B,A,C) ;
E = intersection(s,t) ;
retourne E ;Dans le script principal :
D = point(1,1) ;
E = point(4,2) ;
F = point(2,5) ;
G = gravite(D,E,F){orange,rond2} ;

La fonction mediane est ici de niveau 2 et la fonction gravite de niveau 1.
Bien entendu, une même macro peut être de plusieurs niveaux.
Les points D, E et F sont construits.
En ligne4, on appelle la fonction gravite, qui renvoie le point E, intersection des deux médianes.
Comme on peut le constater, la fonction gravite fait appel à la fonction mediane.
Par défaut, tous les objets contruits par les macros sont invisibles (un paramètre i est ajouté automatiquement par Tep).
Si toutefois, on désire faire apparaître un objet de la macro, il suffit d’ajouter des options de mise en forme.
Cette fonctionnalité ne fonctionne pas de manière satisfaisante dans les macros de niveau 2 comme la macro médiane.
Voici un autre exemple illustant cette technique.
Exemple 2
fonction triangle(A,B,C,x) ;
D& =pointsur(A,B,x) (sansnom,rond2,rouge} ;
E& =pointsur(B,C,x) (sansnom,rond2,rouge} ;
F& =pointsur(C,A,x) (sansnom,rond2,rouge} ;
sE&F& =segment(E&,F&) ;
sF&D& =segment(F&,D&) ;
sD&E& =segment(D&,E&) ;
tr& =polygone(D&,E&,F&) ;
retourne tr&;Dans le script principal :
@options ;@figure ;
R = point(2.27,1.88) ;
T = point(4.82,1.98) ;
var x =RT/10 {0.255196003103497} ;
A = point(0.8,-2.22) ;
B = point(6.4,-2.22) ;
C = point(3.57,0.68) ;
sAB =segment(A,B) ;
sBC =segment(B,C) ;
sCA =segment(C,A) ;
trx =triangle(A,B,C,x) {vertfonce} ;
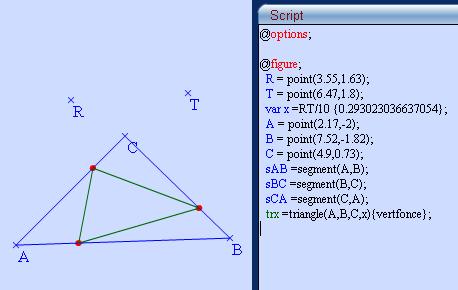
Cette fonction construit un triangle inscrit dans un triangle ABC. Le triangle obtenu est semblable à ABC.
Et il est dessiné en vert foncé.
On peut se demander pourquoi choisir des noms aussi curieux pour les objets internes de la fonction.
Pourquoi tout simplement ne pas écrire :
fonction triangle(A,B,C,x) ;
D =pointsur(A,B,x) {sansnom,rond2,rouge} ;
La raison est qu’il y aura un conflit de nom entre le paramètre de la fonction et l’objet interne dans le cas où l’appel est le suivant :
trx =triangle(D,E,F,x) {vertfonce} ;
Donc, dans les fonctions, il faut utiliser des noms d’objets qui ne risquent pas d’être également des paramètres.
Normalement, tous les objets intermédiaires construits par la fonction sont invisibles ; c’est le cas si aucune option n’est spécifiée.
Mais ici, on a D& =pointsur(A,B,x)(sansnom,rond2,rouge ; Donc cet objet sera dessiné à l’écran puisqu’il y a des options.
Les noms des objets construits par les fonctions sont complexes. Dans le cas présent, l’objet D& a pour nom interne v_point_1_d&.
Par conséquent, il n’est pas question d’afficher son nom. On voit bien sur la figure les trois disques rouges créés par la fonction triangle.
Si on veut tracer le segment reliant le point T et un de ces trois points, alors il est impossible de le faire à paritr du script évidemment.
Il faut utiliser la souris. Même si l’objet pointrouge n’apparaît pas dans le script, il est bien réel et est détecté par la souris.
Créons un de ces segments :
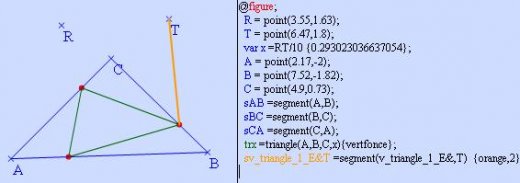
Le segment apparaît alors dans le script. Et le nom du point rouge apparaît !
Ce n’est pas formidable, j’en conviens, mais je n’ai pas trouvé mieux pour le moment...
Sauvegarde et chargement
Les fonctions sont stockées dans des fichiers texte :
Par exemple, dans le répertoire courant de trancempoche.swf, on crée le fichier macros.txt suivant :
fonction mediane(A,B,C) ;
// mediane issue de A dans le triangle ABC ;
I=milieu(B,C) ;
s=segment(A,I) ;
retourne s ;
fonction gravite(A,B,C) ;
s=mediane(A,B,C) ;
t=mediane(B,A,C) ;
E=intersection(s,t) ;
retourne E ;
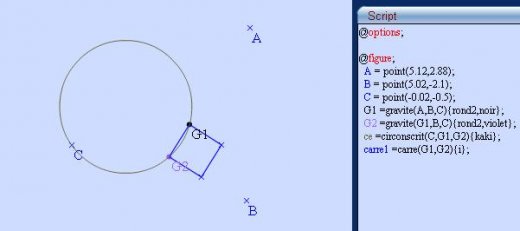
fonction circonscrit(A,B,C) ;
d1=mediatrice(A,B) ;
d2=mediatrice(B,C) ;
E=intersection(d1,d2) ;
ce=cercle(E,A) ;
retourne ce ;
fonction carre(A,B) ;
rA = rotation(A,90) ;
rB = rotation(B,-90) ;
D12=image(rA,B {v,sansnom} ;
C12=image(rB,A {v,sansnom} ;
sAB=segment(A,B {v,sansnom} ;
sBC=segment(B,C12 {v,sansnom} ;
sCD=segment(C12,D12 {v,sansnom} ;
sDA=segment(D12,A {v,sansnom} ;
sAC12=segment(A,C12) ;
sBD12=segment(B,D12) ;
O=intersection(sAC12,sBD12) ;
retourne O ;
fonction triangle(A,B,C,x) ;
D& =pointsur(A,B,x {sansnom,rond2,rouge} ;
E& =pointsur(B,C,x {sansnom,rond2,rouge} ;
F& =pointsur(C,A,x {sansnom,rond2,rouge} ;
sE&F& =segment(E&,F&) ;
sF&D& =segment(F&,D&) ;
sD&E& =segment(D&,E&) ;
tr& =polygone(D&,E&,F&) ;
retourne tr&;
On peut avoir plusieurs fichiers de macros comme ce dernier : macros.txt , macros2.txt , macros3.txt.
TracenPoche charge ces différents fichiers en lisant le fichier macro.tep qui contient :
macro1=macros.txt ;
macro2=macros2.txt ;
macro3=macros3.txt ;
nombre=3 ;
Exemple
Toutes les fonctions sont alors disponibles une fois TracenPoche chargé. Elles ne sont pas disponibles lors du chargement de la première figure (base.txt).
On peut utiliser autant de fonctions que l’on veut et utiliser les objets retournés par les fonctions comme paramètres pour de nouveaux objets.
Voici un dernier exemple :